이전 포스트에서는 이진 탐색 트리 (binary search tree)를 구현해보았다. 트리는 배열이나 스택, 큐 등의 자료구조와 달리 데이터를 직관적으로 살펴보기 어렵다. 따라서 트리를 위한 별도의 순회 알고리즘이 필요하다.
트리 순회 알고리즘
트리 순회 알고리즘은 트리에 저장된 모든 값을 중복이나 빠짐없이 살펴보고 싶을 때 사용한다. 이진 트리의 순회 방법 중 깊이 우선 순회 방법(Depth First Traversal)으로는 전위 순회(Pre-order traversal), 정위 순회(In-order traversal), 후위 순회(Post-order traversal)가 있으며, 너비 우선 순회 방법(Breadth First Traversal)으로는 레벨 순회가 있다. 이전 포스트에서 구현한 BinarySearchTree() 클래스의 메서드 형태로 아래에 차례로 구현해였다.
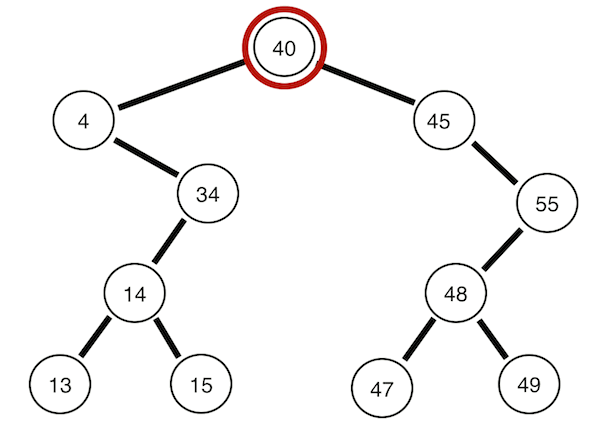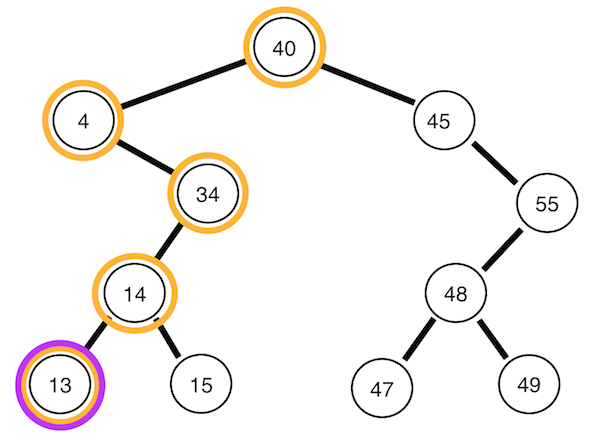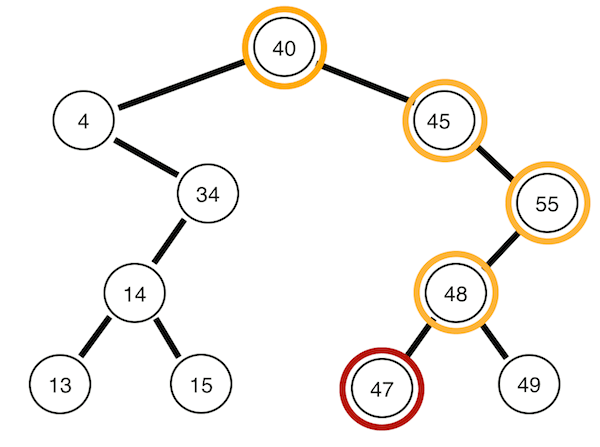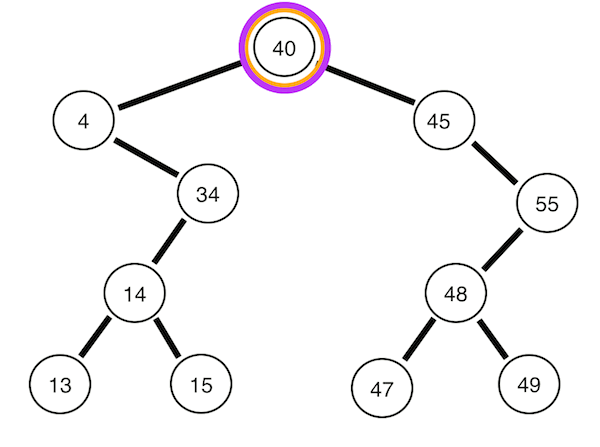
아래의 그림은 모두 [40, 4, 34, 45, 14, 55, 48, 13, 15, 49, 47]의 데이터를 차례로 입력하여 만든 이진 탐색 트리이다.
1. 깊이 우선 순회 (Depth First Traversal)
1.1. 전위 순회 (Pre-order traversal)
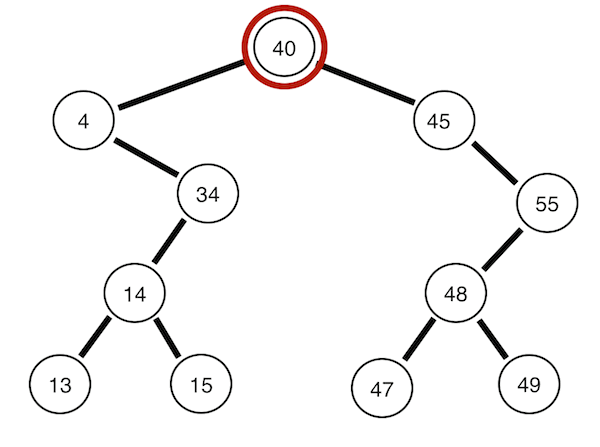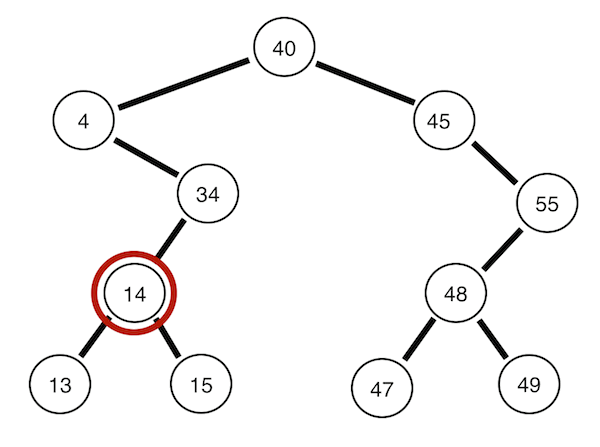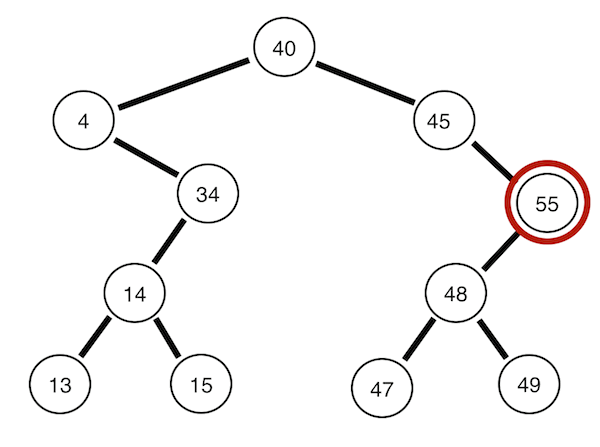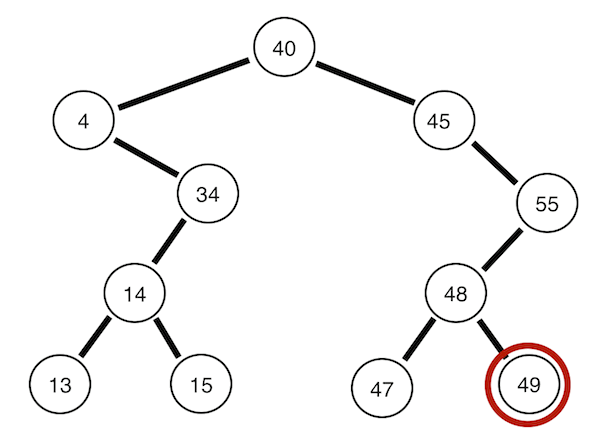
뿌리노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 순회한다. 위의 트리의 경우 40 4 34 14 13 15 45 55 48 47 49의 순서이다.
class BinarySearchTree(object):
...
def pre_order_traversal(self):
def _pre_order_traversal(root):
if root is None:
pass
else:
print(root.data)
_pre_order_traversal(root.left)
_pre_order_traversal(root.right)
_pre_order_traversal(self.root)
1.2. In-order traversal(정위 순회)
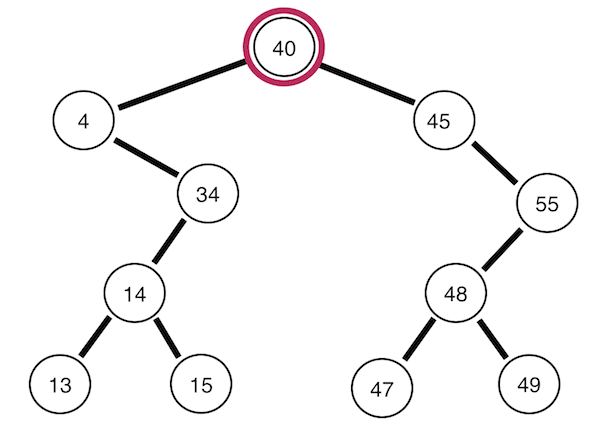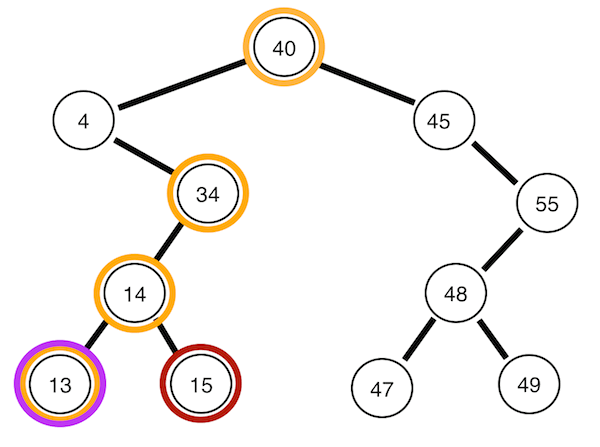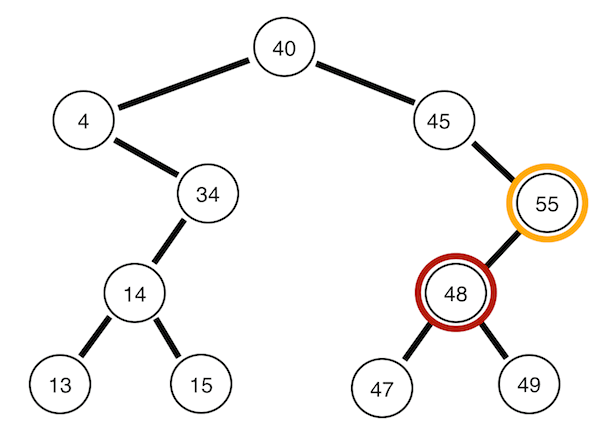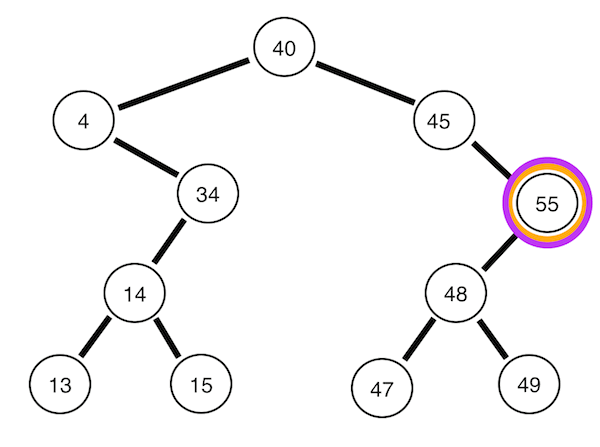
왼쪽 서브트리 -> 뿌리 노드 -> 오른쪽 서브트리 순으로 순회한다. 위의 트리의 경우 4 13 14 15 34 40 45 47 48 49 55의 순서이다. 이진 탐색 트리를 정순회하면 정렬된 데이터를 얻을 수 있다(!)
class BinarySearchTree(object):
...
def in_order_traversal(self):
def _in_order_traversal(root):
if root is None:
pass
else:
_in_order_traversal(root.left)
print(root.data)
_in_order_traversal(root.right)
_in_order_traversal(self.root)
1.3. Post-order traversal(후위 순회)
왼쪽 서브 트리 -> 오른쪽 서브트리 -> 뿌리 노드 순으로 순회한다. 위의 트리의 경우 13 15 14 34 4 47 49 48 55 45 40의 순서이다.
class BinarySearchTree(object):
...
def post_order_traversal(self):
def _post_order_traversal(root):
if root is None:
pass
else:
_post_order_traversal(root.left)
_post_order_traversal(root.right)
print(root.data)
_post_order_traversal(self.root)
2. 너비 우선 순회 (Breadth First Traversal)
2.1. 레벨 순회 (Level-order traversal)
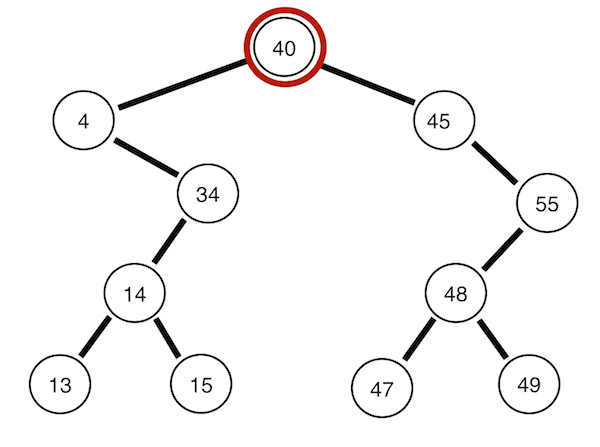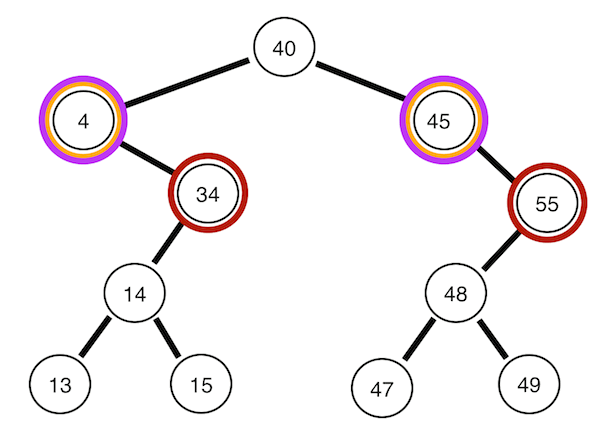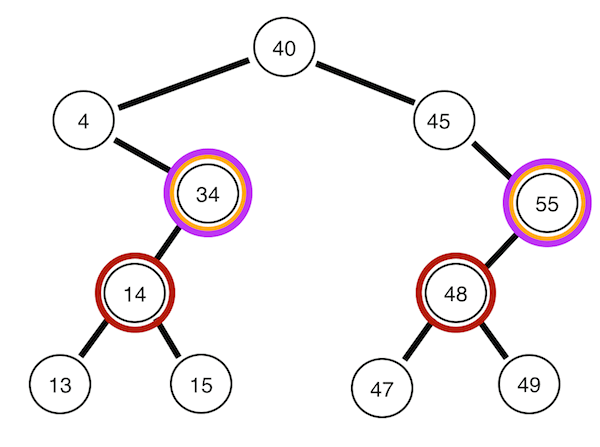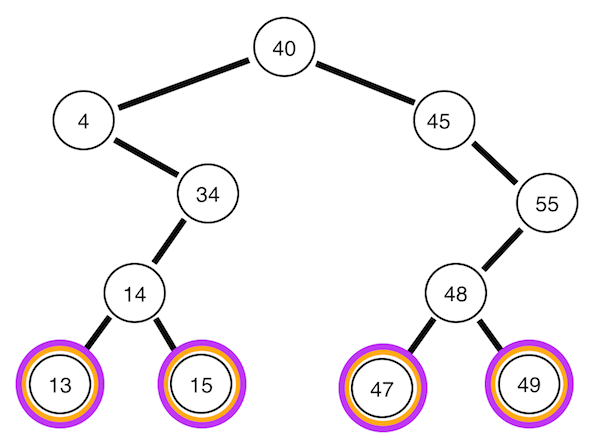
맨 위 뿌리 노드부터 깊이 순으로 방문한다. 아래의 코드는 위의 트리의 노드를 40 4 45 34 55 14 48 13 15 47 49의 순으로 방문한다.
class BinarySearchTree(object):
...
def level_order_traversal(self):
def _level_order_traversal(root):
queue = [root]
while queue:
root = queue.pop(0)
if root is not None:
print(root.data)
if root.left:
queue.append(root.left)
if root.right:
queue.append(root.right)
_level_order_traversal(self.root)
참고로, 너비 우선 탐색(DFS)과 깊이 우선 탐색(BFS) 알고리즘은 트리를 포함하여 각종 그래프를 순회하는 데 사용할 수 있다. 트리는 그래프와 달리 사이클을 가지지 않기 때문에, 구현시 이미 방문한 노드 (
visited)를 기억할 필요가 없다.
구현 결과 확인
이진 탐색 트리와 그 순회 알고리즘이 준비되었으니, 데이터를 넣어서 확인해보자.
array = [40, 4, 34, 45, 14, 55, 48, 13, 15, 49, 47]
bst = BinarySearchTree()
for x in array:
bst.insert(x)
print(bst.find(15)) # True
print(bst.find(17)) # False
# depth first
bst.pre_order_traversal() # 40 4 34 14 13 15 45 55 48 47 49
bst.in_order_traversal() # 4 13 14 15 34 40 45 47 48 49 55
bst.post_order_traversal() # 13 15 14 34 4 47 49 48 55 45 40
# breadth first
bst.level_order_traversal() # 40 4 45 34 55 14 48 13 15 47 49
bst.delete(55) # True
# depth first
bst.pre_order_traversal() # 40 4 34 14 13 15 45 48 47 49
bst.in_order_traversal() # 4 13 14 15 34 40 45 47 48 49
bst.post_order_traversal() # 13 15 14 34 4 47 49 48 45 40
# breadth first
bst.level_order_traversal() # 40 4 45 34 48 14 47 49 13 15
bst.delete(14) # True
# depth first
bst.pre_order_traversal() # 40 4 34 15 13 45 48 47 49
bst.in_order_traversal() # 4 13 15 34 40 45 47 48 49
bst.post_order_traversal() # 13 15 34 4 47 49 48 45 40
# breadth first
bst.level_order_traversal() # 40 4 45 34 48 15 47 49 13
bst.delete(11) # False
# depth first
bst.pre_order_traversal() # 40 4 34 15 13 45 48 47 49
bst.in_order_traversal() # 4 13 15 34 40 45 47 48 49
bst.post_order_traversal() # 13 15 34 4 47 49 48 45 40
# breadth first
bst.level_order_traversal() # 40 4 45 34 48 15 47 49 13