이진 트리 (binary tree)는 최대 두 개의 자식 노드를 가지는 트리 형태의 자료구조로서, 단순히 값을 저장하기 위한 용도로 사용되기 보다는 효율적인 탐색 혹은 정렬을 위해 사용된다. 이진 탐색 트리 (binary search tree)를 사용하면 주어진 값 혹은 이보다 작거나 큰 값들을 평균 $O(\log n)$의 시간복잡도로 찾을 수 있다. 이진 트리의 일종인 힙(heap)을 사용하는 힙 정렬(heap sort)은 $O(n\log n)$의 시간복잡도를 가진다.

이진 탐색 트리 구현

이진 탐색 트리 (binary search tree)는 이진 트리의 특수한 경우이다. 모든 노드에 대해 그 왼쪽 자식들의 값이 현재 노드 값보다 작거나 같으며, 그 오른쪽 자식들의 값이 현재 노드의 값보다 크다는 조건을 만족하면 이진 탐색 트리가 된다.

아래 그림은 [21, 28, 14, 32, 25, 18, 11, 30, 19, 15]의 순서로 주어지는 값으로부터 이진 탐색 트리를 구축하는 과정을 보여준다. 맨 먼저 입력된 값이 뿌리(root) 노드가 되며, 그 다음부터는 입력값과 노드 간 대소관계에 따라 입력값의 노드 위치가 결정된다.

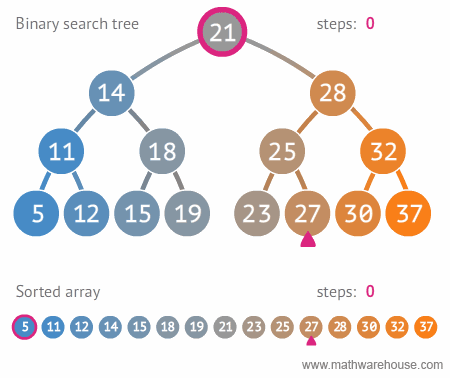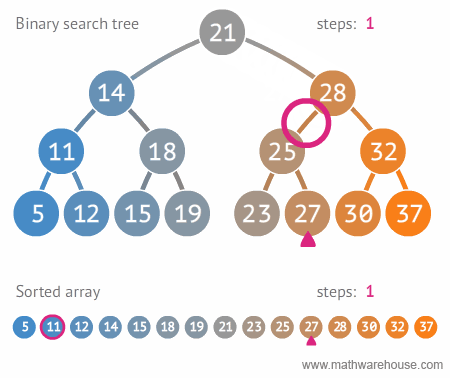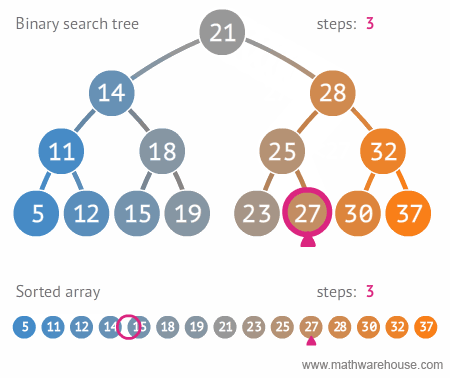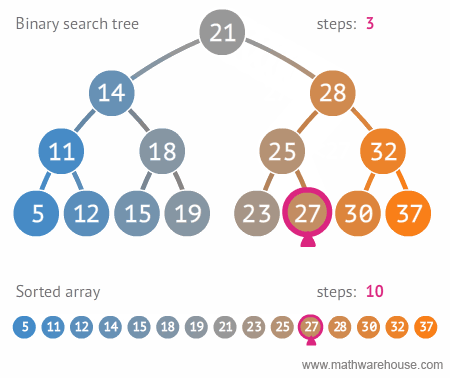
아래 그림은 위와 같이 만든 이진 탐색 트리에서 27을 찾는 과정을 보여준다. 이진 탐색 트리가 정렬된 배열보다 효과적으로 원하는 값을 찾음을 확인할 수 있다1.

(1) 클래스 정의, 초기화

이진 탐색 트리를 구현하려면 먼저 그 재료가 되는 Node 클래스를 정의해야 한다. Node 클래스는 노드값(self.data)과 좌/우 노드(self.left, self.right), 총 세 개의 속성을 가진다. 초기화할 때는 데이터 값만 주어지고 좌우 노드가 비어있다.

class Node(object):
    def __init__(self, data):
        self.data = data
        self.left = self.right = None

이제 Node 클래스를 사용해 이진 탐색 트리 클래스인 BinarySearchTree를 구현해보자. 처음에는 비어 있는 트리이다.

class BinarySearchTree(object):
    def __init__(self):
        self.root = None

이제 여기에 원소를 추가, 삭제, 탐색할 수 있도록 insert(), delete(), find() 메서드를 추가해야 한다.

(2) 삽입 메서드

BinarySearchTree에 insert() 메서드를 구현하여 트리에 새 원소를 추가할 수 있도록 해보자. 재귀를 사용하면 쉽다. 새로 추가할 원소의 값을 현재 노드의 값과 비교하여 왼쪽/오른쪽 중 알맞은 위치로 노드를 옮겨가며 삽입 위치를 체크한다.

class BinarySearchTree(object):
    ...
    def insert(self, data):
        self.root = self._insert_value(self.root, data)
        return self.root is not None

    def _insert_value(self, node, data):
        if node is None:
            node = Node(data)
        else:
            if data <= node.data:
                node.left = self._insert_value(node.left, data)
            else:
                node.right = self._insert_value(node.right, data)
        return node

(3) 탐색 메서드

원하는 값의 존재유무를 확인할 수 있도록 find() 메서드를 구현해보자. 이 역시 재귀와 값의 대소관계 비교를 통해 쉽게 구현할 수 있다.

class BinarySearchTree(object):
    ...
    def find(self, key):
        return self._find_value(self.root, key)

    def _find_value(self, root, key):
        if root is None or root.data == key:
            return root is not None
        elif key < root.data:
            return self._find_value(root.left, key)
        else:
            return self._find_value(root.right, key)

(4) 삭제 메서드

삭제는 비교적 까다롭다. 왜 그럴까?

삭제할 노드의 자식이 없으면 문제가 없다. 자식이 하나인 경우엔 자식 노드를 삭제한 노드 위치로 가져오면 된다. 그러나, 삭제할 노드의 자식이 두개일 때는 어느 자식 노드를 어떻게 가져와야 할까?

왼쪽 서브 트리와 오른쪽 서브 트리를 각각 A, B라고 하자. 이 때, B에서 가장 왼쪽 아래에 위치한 자손을 가져오면 된다! 이 원소는 A의 모든 원소들보다 크면서, B의 나머지 원소보다 작다.

class BinarySearchTree(object):
    ...
    def delete(self, key):
        self.root, deleted = self._delete_value(self.root, key)
        return deleted

    def _delete_value(self, node, key):
        if node is None:
            return node, False

        deleted = False
        if key == node.data:
            deleted = True
            if node.left and node.right:
                # replace the node to the leftmost of node.right
                parent, child = node, node.right
                while child.left is not None:
                    parent, child = child, child.left
                child.left = node.left
                if parent != node:
                    parent.left = child.right
                    child.right = node.right
                node = child
            elif node.left or node.right:
                node = node.left or node.right
            else:
                node = None
        elif key < node.data:
            node.left, deleted = self._delete_value(node.left, key)
        else:
            node.right, deleted = self._delete_value(node.right, key)
        return node, deleted

이진 트리의 좌우 균형이 맞으면 탐색/삽입/삭제의 시간복잡도가 $O(\log n)$이다. 그러나 이진 탐색 트리는 정렬된 데이터에 취약하다. 오름차순이든 내림차순이든 정렬된 데이터가 입력되면 한쪽으로 치우친 (skewed) 트리가 만들어진다. 이 때, 최악의 경우 모든 데이터를 살펴야 할 수도 있어 시간복잡도가 $O(n)$이 된다.

결과 확인

예제를 통해 구현 결과를 확인해보자.

array = [40, 4, 34, 45, 14, 55, 48, 13, 15, 49, 47]

bst = BinarySearchTree()
for x in array:
    bst.insert(x)

# Find
print(bst.find(15)) # True
print(bst.find(17)) # False

# Delete
print(bst.delete(55)) # True
print(bst.delete(14)) # True
print(bst.delete(11)) # False

그런데, 트리 안에 어떤 원소들이 담겨 있는지 어떻게 확인해야 할까?

트리는 그 구조의 특성상 저장된 원소들을 하나씩 살펴보기 위해 별도의 순회 알고리즘이 필요하다. 트리 순회 알고리즘은 다음 포스트에서 살펴보자.

참고

  1. 이미 정렬된 배열인데도 이진 탐색이 아닌 순차 탐색을 사용한 이유는 이진 탐색 트리가 더 효율적인 것처럼 보이기 위함이겠지..? ↩