탐색과 정렬 알고리즘은 서로 뗄레야 뗄 수 없는 사이다. 원하는 값을 찾을 때까지 값을 차례로 살펴보는 순차탐색(sequential search)은 데이터가 정렬되어 있지 않아도 사용할 수 있지만 $O(n)$이다. 데이터를 절반씩 버리면서 원하는 값을 찾아나가는 이진탐색(binary search)은 $O(\log n)$으로 시간복잡도가 낮지만 데이터가 순서에 맞게 정렬되어 있어야 한다는 제약이 있다. 따라서 효율적인 정렬 알고리즘이 필수다. 아래는 기본적으로 알아두면 좋은 정렬 알고리즘의 성능을 요약한 표이다.
| Name | Best | Worst | Stable | Memory |
|---|---|---|---|---|
| 버블정렬 | $n$ | $n^2$ | True | 1 |
| 선택정렬 | $n^2$ | $n^2$ | False | 1 |
| 삽입정렬 | $n$ | $n^2$ | True | 1 |
| 셸정렬 | $n\log n$ | (best) $n \log ^2 n$ | False | 1 |
| 병합정렬 | $n\log n$ | $n\log n$ | True | $n$ |
| 퀵정렬 | $n\log n$ | $n\log n$ ~ $n^2$ | False | $\log n$ ~ $n$ |
아래에 각 정렬 알고리즘을 차례로 설명하였다. 꿀벌이 꽃을 옮기는 비유가 꽤 맘에 들어 가져왔는데, 선택정렬, 병합정렬, 퀵정렬에 해당하는 비유는 없어서 아쉽다.
Bubble Sort (버블정렬)
이웃한 두 값을 비교하여 정렬한다. 큰 값이 오론쪽으로 이동하는 과정이 반복되면서 비교했던 모든 값들의 최댓값이 맨 오른쪽으로 옮겨지게 된다.
최악의 경우 $(n-1) + (n-2) + \cdots + 1$번 비교가 이루어지므로 $O(n^2)$이다. 그러나, 데이터가 잘 졍렬돼있다면 $O(n)$이므로 데이터의 정렬 여부를 파악하기 위한 알고리즘으로 사용될 수 있다. Short Bubble sort는 데이터 정렬이 완료되면 early stopping한다.
def swap(x, i, j):
x[i], x[j] = x[j], x[i]
def bubbleSort(x):
for size in reversed(range(len(x))):
for i in range(size):
if x[i] > x[i+1]:
swap(x, i, i+1)
Selection Sort (선택정렬)
주어진 배열에서 최댓값(최솟값)을 찾아 맨 오른쪽(왼쪽)값과 교체한다. 최댓값을 맨 오른쪽으로 보낸다는 점에서 버블정렬과 비슷하지만, 이웃한 두 값을 정렬하는 과정이 없기 때문에 대체로 버블정렬보다 빠르다. 최댓값을 찾아야 하므로 정렬 상태에 관계없이 언제나 $O(n^2)$이다.

def swap(x, i, j):
x[i], x[j] = x[j], x[i]
def selectionSort(x):
for size in reversed(range(len(x))):
max_i = 0
for i in range(1, 1+size):
if x[i] > x[max_i]:
max_i = i
swap(x, max_i, size)
Insertion Sort (삽입정렬)
아직 정렬되지 않은 값을 이미 정렬된 배열 사이에 끼워 넣는 과정을 반복한다. 여전히 $O(n^2)$이지만 평균적으로 삽입정렬이 선택정렬과 버블정렬에 비해 빠르다.
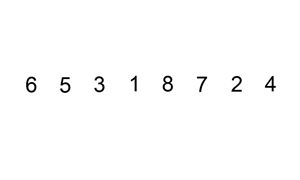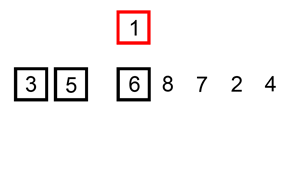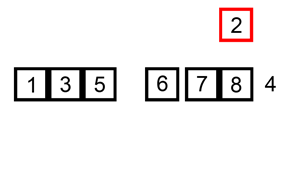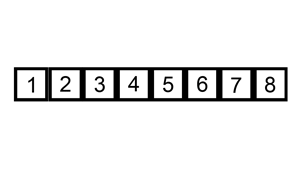
버블정렬과 마찬가지로 데이터가 이미 정렬되어 있다면 $O(n)$이다. 그러나, 데이터가 역순으로 정렬된 상태라면 삽입을 위해 값을 하나씩 뒤로 밀어내는 과정을 아주 많이 반복해야 하므로 느리다..
def insertionSort(x):
for size in range(1, len(x)):
val = x[size]
i = size
while i > 0 and x[i-1] > val:
x[i] = x[i-1]
i -= 1
x[i] = val
Shell Sort (셸 정렬)
삽입 정렬이 거의 정렬된 배열에서 최적의 성능을 냄과 동시에 값 하나씩 위치를 결정하여 비효율적이라는 점에서 착안되었다. 셸 정렬은 주어진 간격만큼 듬성듬성 떨어진 서브배열을 만들어 삽입정렬을 수행한다. 간격이 3이라면 3개의 서브배열이 만들어진다. 모든 서브배열에 대해 삽입정렬을 마쳤다면, 간격을 (보통 절반으로) 줄여 반복한다. 간격이 1이 되면 거의 정렬이 된 상태이므로 빠르게 정렬할 수 있다.
간격 정의에 따라 성능이 제각각이라 시간복잡도 분석이 쉽지 않다. 배열이 이미 정렬되어 있다면 $O(n\log n)$이고 최악의 경우 아래 구현처럼 간격을 절반씩 줄인다면 $O(n^2)$이다. 다른 간격 정의를 사용한다 하더라도 현재까지 알려진 바로는 $O(n \log ^2 n)$이 최선이다.
def gapInsertionSort(x, start, gap):
for target in range(start+gap, len(x), gap):
val = x[target]
i = target
while i > start:
if x[i-gap] > val:
x[i] = x[i-gap]
else:
break
i -= gap
x[i] = val
def shellSort(x):
gap = len(x) // 2
while gap > 0:
for start in range(gap):
gapInsertionSort(x, start, gap)
gap = gap // 2
Merge Sort (병합 정렬)
폰 노이만이 개발했으며, 두 부분으로 쪼개는 작업을 재귀적으로 반복한 뒤, 쪼갠 순서의 반대로 작은 값부터 병합해나가는 분할 정복 알고리즘의 일종이다.
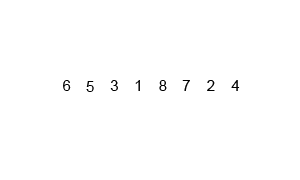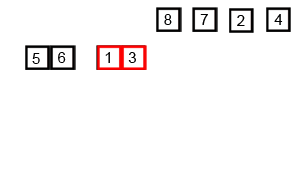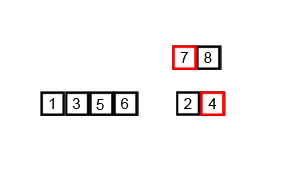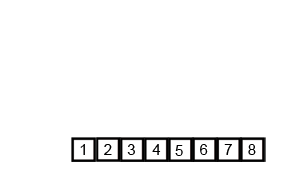
두 부분으로 쪼개는 데 $O(\log n)$ (이진탐색 참고)이고, 데이터 병합이 $O(n)$이므로, 정렬 상태와 무관하게 언제나 $O(n\log n)$이다. 데이터 크기만한 메모리가 더 필요한 게 단점이다.
def mergeSort(x):
if len(x) > 1:
mid = len(x)//2
lx, rx = x[:mid], x[mid:]
mergeSort(lx)
mergeSort(rx)
li, ri, i = 0, 0, 0
while li < len(lx) and ri < len(rx):
if lx[li] < rx[ri]:
x[i] = lx[li]
li += 1
else:
x[i] = rx[ri]
ri += 1
i += 1
x[i:] = lx[li:] if li != len(lx) else rx[ri:]
Quick Sort (퀵 정렬)
피벗(pivot, 기준값) 원소를 정하여 피벗보다 작은 값은 피벗 앞 쪽에, 피벗보다 큰 값은 피벗 뒤 쪽에 오도록 한다. 피벗 양 쪽 배열에 대해 같은 작업을 반복해나간다. 분할 정복 방법의 일종이며, 재귀 호출이 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해진다. 병합정렬은 데이터를 쪼갠 뒤 합치는 과정에서 정렬하지만, 퀵정렬은 데이터를 쪼개면서 정렬한다.
데이터를 절반씩 쪼갠다면 $O(\log n)$이고 $n$개의 값을 피봇과 비교하므로 $O(n\log n)$이다. 피봇 선정 기준에 따라 쪼개는 위치가 한 쪽에 치우쳐 있을 수도 있다 (예: 데이터가 이미 정렬되어 있고, 맨 끝 원소를 피봇으로 선정하는 경우). 이 때는 쪼개는 비용이 $O(n)$이므로 퀵정렬의 시간복잡도가 $O(n^2)$까지 증가한다. 재귀 호출을 위한 스택을 사용하므로 추가 메모리가 필요하다.
def swap(x, i, j):
x[i], x[j] = x[j], x[i]
def pivotFirst(x, lmark, rmark):
pivot_val = x[lmark]
pivot_idx = lmark
while lmark <= rmark:
while lmark <= rmark and x[lmark] <= pivot_val:
lmark += 1
while lmark <= rmark and x[rmark] >= pivot_val:
rmark -= 1
if lmark <= rmark:
swap(x, lmark, rmark)
lmark += 1
rmark -= 1
swap(x, pivot_idx, rmark)
return rmark
def quickSort(x, pivotMethod=pivotFirst):
def _qsort(x, first, last):
if first < last:
splitpoint = pivotMethod(x, first, last)
_qsort(x, first, splitpoint-1)
_qsort(x, splitpoint+1, last)
_qsort(x, 0, len(x)-1)
퀵정렬은 병합정렬과 달리 데이터를 복제할 필요가 없는 in-place 알고리즘이다. 하지만, 퀵정렬의 파이썬 구현을 인터넷에 검색해보면 데이터를 복제하여 O(n)의 추가 메모리를 사용하는 방식으로 구현한 코드가 많다. 이렇게 구현하면 추가 메모리를 사용하긴 하지만 실행속도가 빨라지며 stable한 퀵정렬이 된다. stable의 의미를 모른다면 아래 나무위키 글을 참고하자.
파이썬은 퀵정렬을 하지 않는다. 그 이유는 파이썬은 stable한 정렬을 하는데, 퀵정렬은 stable하지 않기 때문이다. 예를 들어 한글의 키값이 2, 숫자의 키값이 1이라 두면 1, ㄱ , ㄷ, ㄹ, 2를 퀵정렬해서 2, 1, ㄹ, ㄱ, ㄷ 같은 게 나올 수도 있다. O(n)의 추가 메모리를 이용하면 stable한 퀵정렬을 만들 수 있다.
가상 데이터를 사용한 실험
아래의 총 3가지 가상 데이터를 생성하여 정렬 알고리즘 코드 실행시간을 비교했다.
- sortedData: 오름차순 데이터
- randomData: 임의 순서의 데이터
- reversedData: 내림차순 데이터
데이터 크기를 100, 200, 400, 800, 1600의 5가지로 설정하였다. 설정 별로 총 30번 수행하였으며, 실행시간 평균을 시각화하였다.
1. $O(n^2)$ 알고리즘 결과
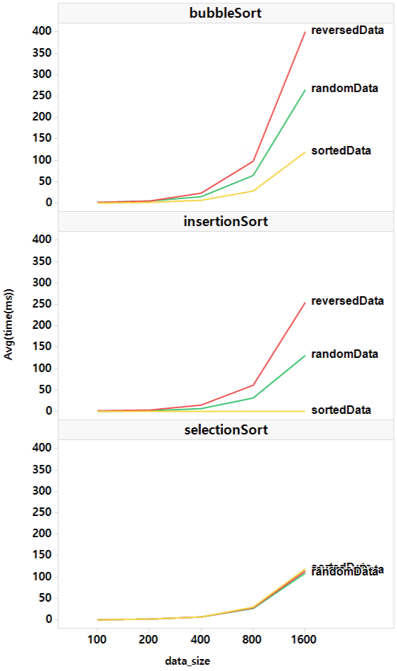
데이터 크기가 커질수록 실행시간이 가파르게 증가한다. 단, 정렬된 데이터에서는 삽입정렬이 매우 빠르다. 선택정렬은 데이터 정렬상태에 관계없이 늘 같은 시간이 소요된다.
2. $O(n \log n)$ 알고리즘 결과
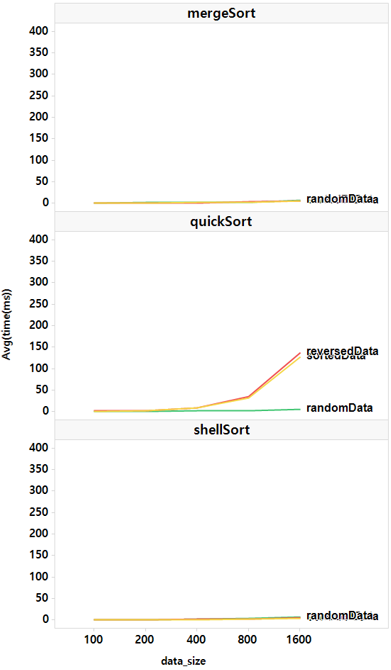
세 알고리즘 모두 매우 빠르지만, 퀵정렬에서는 예외가 있다. 오름차순이든 내림차순이든 정렬된 데이터에선 퀵정렬이 느리다. 왜 그럴까? 위의 구현에서 첫 번째 값를 피벗으로 선택했기 때문이다. 데이터가 절반으로 나눠지지 않고 한쪽으로 몰리기 때문에 쪼개는 비용이 $O(n)$이 되어 $O(n^2)$의 알고리즘이 되었다.
만약 배열의 첫 번째 값, 중간에 위치한 값, 맨 끝 값 중 중앙값(median)을 피벗으로 선택하면 어떻게 될까? 또한, 무작위로 피벗을 정하면 어떻게 될까? 각각 실험하여 아래 그림에 quickSort2, quickSort3로 표시하여 정리하였다.
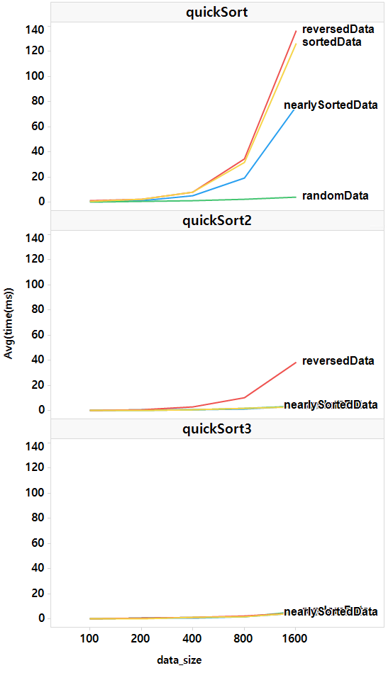
이번에는 nearly sorted 데이터도 한 번 추가해봤다. 피벗으로 중앙값을 선택한 quickSort2를 보면 reversedData가 여전히 느리다. 데이터가 절반으로 나눠지긴 했지만, 데이터가 역순으로 정렬되어 있어 피벗 양쪽의 값을 서로 교환하는 비용이 발생하기 때문에 어쩔 수 없다.
피벗으로 임의의 값을 선택한 quickSort3는 모든 경우의 데이터에서 빠르다. 크기 1600의 randomData에서 병합정렬과 셸정렬 모두 평균 7.03초인데 반해 퀵정렬(quickSort3)은 평균 5.47초가 소요되었다!